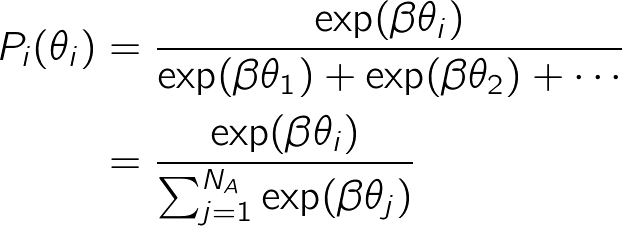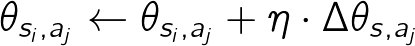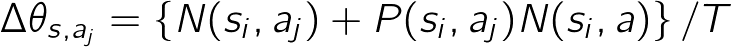2018.01.23
作りながら学ぶ強化学習 -初歩からPyTorchによる深層強化学習まで
第5回 ⽅策勾配法で迷路を攻略
SEやプログラマ、エンジニア、一般の方を対象に、少しずつ実際にプログラムを作りながら、強化学習および深層強化学習について解説していきます。
本連載をまとめ、さらに多くの記事を追加した書籍『つくりながら学ぶ!深層強化学習』を2018年7月に発売しました!
はじめに
前回は、エージェントの行動ルールである方策πθ (s,a)という概念の導入、迷路課題を対象に表形式で方策πθ0 (s,a)を実装、エージェントが方策に従いゴールを目指す部分の実装、エージェントの移動軌跡を動画で可視化する部分の実装を解説しました。
今回は強化学習のアルゴリズムの一種である方策勾配法を用いて、エージェントが一直線にゴールへ向かうように方策を学習させます。
強化学習の方法
2種類のアルゴリズム
前回実装した迷路課題ではエージェントがランダムに行動してゴールにたどり着きました。エージェントが一直線にゴールへ向かうようにするには、どう学習させれば良いのか、少し考えてみましょう。
いろいろな方法が思い浮かぶかもしれませんが、大きく2つの方法があります。
1つ目の方法は方策に従って行動しゴールにたどり着いたときに、早くゴールできたケースで実行した行動(action)は重要だと考え、その行動を今後多く取り入れるように方策を更新する作戦です。つまり、うまくいったケースの行動を重要視する作戦です。
2つ目の方法はゴールから逆算して、ゴールの1つ手前、2つ手前の位置(状態)へと順々に誘導していく作戦です。つまり、ゴール以外の位置(状態)にも価値(優先度)をつけてあげる作戦です。
実はこれら2つの作戦には名前があり、1つ目の方法は方策反復法、2つ目の方法は価値反復法と呼ばれます。今回は1つ目の方策反復法の具体的アルゴリズムである方策勾配法(Policy Gradient Method)を実装します。
方策勾配法の実装
準備
前回の実装コードをロードしていただくか、以下のセルを実行してください。
# Jupyterでmatplotlibを使用する宣言と、使用するライブラリの定義 import numpy as np import matplotlib.pyplot as plt %matplotlib inline
# 初期位置での迷路の様子
# 図を描く大きさと、図の変数名を宣言
fig = plt.figure(figsize=(5, 5))
ax = plt.gca()
# 赤い壁を描く
plt.plot([1, 1], [0, 1], color='red', linewidth=2)
plt.plot([1, 2], [2, 2], color='red', linewidth=2)
plt.plot([2, 2], [2, 1], color='red', linewidth=2)
plt.plot([2, 3], [1, 1], color='red', linewidth=2)
# 状態を示す文字S0~S8を描く
plt.text(0.5, 2.5, 'S0', size=14, ha='center')
plt.text(1.5, 2.5, 'S1', size=14, ha='center')
plt.text(2.5, 2.5, 'S2', size=14, ha='center')
plt.text(0.5, 1.5, 'S3', size=14, ha='center')
plt.text(1.5, 1.5, 'S4', size=14, ha='center')
plt.text(2.5, 1.5, 'S5', size=14, ha='center')
plt.text(0.5, 0.5, 'S6', size=14, ha='center')
plt.text(1.5, 0.5, 'S7', size=14, ha='center')
plt.text(2.5, 0.5, 'S8', size=14, ha='center')
plt.text(0.5, 2.3, 'START', ha='center')
plt.text(2.5, 0.3, 'GOAL', ha='center')
# 描画範囲の設定と目盛りを消す設定
ax.set_xlim(0, 3)
ax.set_ylim(0, 3)
plt.tick_params(axis='both', which='both', bottom='off', top='off',
labelbottom='off', right='off', left='off', labelleft='off')
# 現在値S0に緑丸を描画する
line, = ax.plot([0.5], [2.5], marker="o", color='g', markersize=60)
# 初期の方策を決定するパラメータtheta_0を設定
# 行は状態0~7、列は移動方向で↑、→、↓、←を表す
theta_0 = np.array([[np.nan, 1, 1, np.nan], # s0
[np.nan, 1, np.nan, 1], # s1
[np.nan, np.nan, 1, 1], # s2
[1, 1, 1, np.nan], # s3
[np.nan, np.nan, 1, 1], # s4
[1, np.nan, np.nan, np.nan], # s5
[1, np.nan, np.nan, np.nan], # s6
[1, 1, np.nan, np.nan], # s7、※s8はゴールなので、方策はなし
])
softmax関数による方策πθ (s,a)の実装
パラメータθから、方策πθ (s,a)を求める関数を実装します。前回の第4回では単純にθを割合に変換して方策を求める関数simple_convert_into_pi_from_thetaを実装しました。今回はこの変換関数を少し変更し、θを変換する際にsoftmax関数を使用します。softmax関数は機械学習、ディープラーニングで頻繁に使用される関数です(その理由についてはまた別の機会で解説したいと思います)。softmax関数は以下の式で記述されます。
NAは選択可能な行動の種類数を示し、今回の迷路の場合は4になります。式が出てきて難しい印象を持たれる方もいるかもしれませんが、単純にθのexponetial(エクスポネンシャル)関数を計算してから割合を求めているだけです。なおθにかかる係数βは逆温度と呼ばれます。逆温度βが小さいほど行動がよりランダムになるという性質があります。
どうして単純な割合の変換ではなく、softmax関数による変換が必要なのかについては、今回の最後で解説します。
それでは関数softmax_convert_into_pi_from_thetaを実装します。
# 方策パラメータthetaを行動方策piにソフトマックス関数で変換する手法の定義
def softmax_convert_into_pi_from_theta(theta):
'''ソフトマックス関数で割合を計算する'''
beta =1.0
[m, n] = theta.shape # thetaの行列サイズを取得
pi = np.zeros((m, n))
exp_theta = np.exp(beta*theta) # thetaをexp(theta)へと変換
for i in range(0, m):
# pi[i, :] = theta[i, :] / np.nansum(theta[i, :]) # simpleに割合の計算の場合
pi[i, :] = exp_theta[i, :] / np.nansum(exp_theta[i, :]) # simpleに割合の計算の場合
pi = np.nan_to_num(pi) # nanを0に変換
return pi
続いて定義した変換関数を実行してθ0から方策πθ0 (s,a)を求めます。
# 初期の方策pi_0を求める pi_0 = softmax_convert_into_pi_from_theta(theta_0) print(pi_0)
実行結果は以下の図5.1のようになります。pi_0の結果は前回と同じくただ割合を計算したものになっています。初期状態では同じ結果になりますが、今後θの値が変わると、関数softmax_convert_into_pi_from_thetaの計算結果は単純な割合計算とは異なる結果になります。
図5.1 softmax関数を使⽤した⽅策πθ0 (s,a)
エージェントがsoftmax方策に従いゴールを目指す部分の実装
続いて、softmax関数による方策πθ (s,a)に従って、エージェントを行動させます。
前回定義した1step移動後のエージェントの状態sを求める関数get_next_sを少し変更します。状態だけでなくそのとき採用した行動(上、右、下、左のいずれか)も取得するようにします。この新しい関数を関数get_action_and_next_sとして定義します。
# 行動と1step移動後の状態sとを求める関数を定義
def get_action_and_next_s(pi, s):
direction = ["up", "right", "down", "left"]
# pi[s,:]の確率に従って、directionが選択される
next_direction = np.random.choice(direction, p=pi[s, :])
if next_direction == "up":
action = 0
s_next = s - 3 # 上に移動するときは状態の数字が3小さくなる
elif next_direction == "right":
action = 1
s_next = s + 1 # 右に移動するときは状態の数字が1大きくなる
elif next_direction == "down":
action = 2
s_next = s + 3 # 下に移動するときは状態の数字が3大きくなる
elif next_direction == "left":
action = 3
s_next = s - 1 # 左に移動するときは状態の数字が1小さくなる
return [action, s_next]
続いてゴールにたどり着くまでエージェントを移動させ続ける関数goal_mazeも少し変更します。前回定義した関数goal_mazeはスタートからゴールまでの状態(位置)の履歴をstate_historyとして出力していました。今回は、状態だけでなくその状態で採用した行動も出力するように変更します。これを関数goal_maze_ret_s_aとして定義します。関数goal_mazeのreturnがstate(状態)とaction(行動)バージョンという意味です。
# 迷路を解く関数の定義、状態と行動の履歴を出力
def goal_maze_ret_s_a(pi):
s = 0 # スタート地点
s_a_history = [[0, np.nan]] # エージェントの移動を記録するリスト
while (1): # ゴールするまでループ
[action, next_s] = get_action_and_next_s(pi, s)
s_a_history[-1][1] = action
# 現在の状態(つまり一番最後なのでindex=-1)の行動を代入
s_a_history.append([next_s, np.nan])
# 次の状態を代入。行動はまだ分からないのでnanにしておく
if next_s == 8: # ゴール地点なら終了
break
else:
s = next_s
return s_a_history
それでは初期の方策πθ0 (s,a)で goal_maze_ret_s_aを実行してみましょう。
s_a_history = goal_maze_ret_s_a(pi_0)
print(s_a_history)
print("迷路を解くのにかかったステップ数は"+str(len(s_a_history)-1)+"です")
すると図5.2のように状態と行動のペアが出力され、トータルで何ステップを要したのか出力されます。
方策勾配法に従い方策を更新する
続いて、方策勾配法に従い方策を更新する部分を実装します。方策勾配法では次の式に従いパラメータθを更新します。
ここでθsi ,ajは状態(位置)siで行動ajを採用する確率を決めるパラメータです。ηは学習係数と呼ばれ、θsi ,ajが学習により更新される度合いをコントロールします。ηが小さすぎるとなかなか学習が進みませんが、大きすぎるときちんと学習できません。N(si,aj)は状態siで行動ajをとった回数です。P(si,aj)は現在の方策で状態siで行動ajをとる確率です。N(si,a)は状態siでなんらか行動した回数の合計です。Tはゴールまでにかかった総ステップ数です。
どうしてこのような更新式が出て来るのかについては、今回の最後で解説します。
それではこの更新を関数update_thetaとして定義します。入力には現在のthetaと方策pi、そして現在の方策での実行結果s_a_historyを使用します。
# thetaの更新関数を定義します
def update_theta(theta, pi, s_a_history):
eta = 0.1 # 学習率
T = len(s_a_history) - 1 # ゴールまでの総ステップ数
[m, n] = theta.shape # thetaの行列サイズを取得
delta_theta = theta.copy() # Δthetaの元を作成、ポインタ参照なので、delta_theta = thetaはダメ
# delta_thetaを要素ごとに求めます
for i in range(0, m):
for j in range(0, n):
if not(np.isnan(theta[i, j])): # thetaがnanでない場合
# 履歴から状態iのものを取り出すリスト内包表記です
SA_i = [SA for SA in s_a_history if SA[0] == i]
SA_ij = [SA for SA in s_a_history if SA ==
[i, j]] # 状態iで行動jをしたものを取り出す
N_i = len(SA_i) # 状態iで行動した総回数
N_ij = len(SA_ij) # 状態iで行動jをとった回数
delta_theta[i, j] = (N_ij + pi[i, j] * N_i) / T
new_theta = theta + eta * delta_theta
return new_theta
上記コードではdelta_thetaを求める際にtheta.copy()という命令を使用しています。numpyは計算の高速化のためにポインタ参照を使用しているため、delta_theta = thetaとしてしまうと、delta_thetaとthetaが同じ内容になってしまいます。すると、片方を更新したときに同時にもう片方も変化してしまいます。この現象を避け別々の変数にするには、変数名.copy()という命令を使用する必要があります。また、リスト内包表記と呼ばれるPythonのテクニックを使用し、リストs_a_historyから状態si のものを取り出しています(その他、SA_iとSA_ijを計算するコードは、それぞれのfor文内のほうが計算コストが低くなりますが、分かりやすさを優先して現在の位置で記述しています)。
それでは関数update_thetaを実行して、パラメータθを更新し、方策πθがどう変化するのか見てみましょう。
new_theta = update_theta(theta_0, pi_0, s_a_history) pi = softmax_convert_into_pi_from_theta(new_theta) print(pi)
更新結果は以下の図5.3のようになります。行動がランダムなので、細かい数字は実行のたびに変わりますが、最初の一様な行動確率からは少し変化しているはずです。
方策勾配法で迷路を解く実装
最後に迷路を一直線にクリアできるまで迷路内の探索とパラメータθの更新を繰り返す部分を実装します。
# 方策勾配法で迷路を解く
stop_epsilon = 10**-8 # 10^-8よりも方策に変化が少なくなったら学習終了とする
theta = theta_0
pi = pi_0
is_continue = True
count = 1
while is_continue: # is_continueがFalseになるまで繰り返す
s_a_history = goal_maze_ret_s_a(pi) # 方策πで迷路内を探索した履歴を求める
new_theta = update_theta(theta, pi, s_a_history) # パラメータΘを更新
new_pi = softmax_convert_into_pi_from_theta(new_theta) # 方策πの更新
print(np.sum(np.abs(new_pi - pi))) # 方策の変化を出力
print("迷路を解くのにかかったステップ数は" + str(len(s_a_history) - 1) + "です")
if np.sum(np.abs(new_pi - pi)) < stop_epsilon:
is_continue = False
else:
theta = new_theta
pi = new_pi
実行すると以下の図5.4のように、各試行のステップ数と、方策πの変化の絶対値和が出力されます。学習終了の条件をどう設定するかですが、今回は方策の変化が10-8よりも小さくなったらと終了としました。学習終了条件は課題に合わせて調整する必要があります。
最終的な方策の内容を確認してみましょう。
np.set_printoptions(precision=3, suppress=True) #有効桁数3、指数表示しないという設定 print(pi)
以下の図5.5のような方策が得られました。方策の2, 3行目(状態1, 2)はスタートから右に行った行き止まり方向です。初期には迷い込むことがあっても最終的には進入することがないため微妙な数字になっています。その他の状態では各行動が1か0になっており、状態によって採用する行動が確定しています。
最後に前回と同様に動画でエージェントの移動を可視化します。入力していただくコードは前回とほぼ同じですが、s_a_historyを使用するよう変更しています。動画を見ると、さまようことなく一直線にゴールに向かっており、うまく強化学習で迷路を解くことができていることが分かります。
# エージェントの移動の様子を可視化します
# 参考URL http://louistiao.me/posts/notebooks/embedding-matplotlib-animations-in-jupyter-notebooks/
from matplotlib import animation
from IPython.display import HTML
def init():
# 背景画像の初期化
line.set_data([], [])
return (line,)
def animate(i):
# フレームごとの描画内容
state = s_a_history[i][0] # 現在の場所を描く
x = (state % 3) + 0.5 # 状態のx座標は、3で割った余り+0.5
y = 2.5 - int(state / 3) # y座標は3で割った商を2.5から引く
line.set_data(x, y)
return (line,)
# 初期化関数とフレームごとの描画関数を用いて動画を作成
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=len(
s_a_history), interval=200, repeat=False)
HTML(anim.to_html5_video())
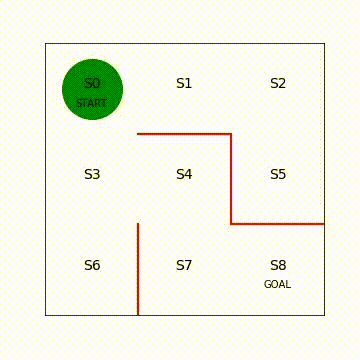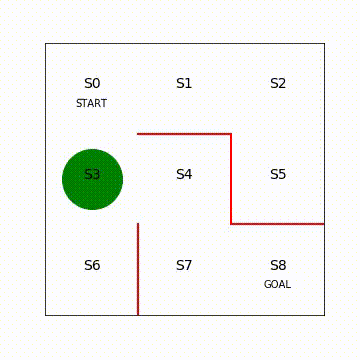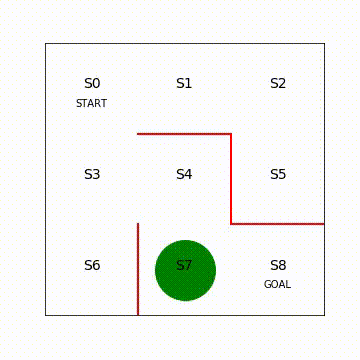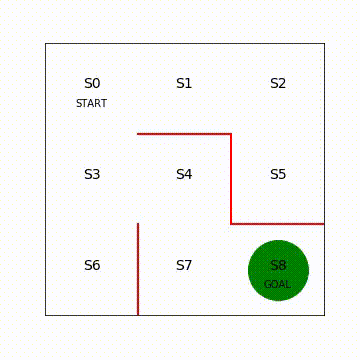
図5.6 強化学習後のエージェントの移動の様⼦(再⽣繰り返し)
以上で方策勾配法により迷路を解く強化学習プログラムの実装ができました。
方策勾配法の理論
ここまで実際に方策勾配法で迷路を解く強化学習を実装しました。ですが、少し疑問が残っていると思います。
「なぜ方策を求めるときに、softmax関数を使用したのか?」
「なぜθの更新式は今回使用した式の形で記述されたのか?」
これらの疑問について簡単に答えます。
今回の迷路課題のように方策を表形式表現で表した場合、softmax関数を使用してパラメータθから方策πへの変換を行うと、パラメータθが負の値になっても確率が計算できるという利点があります。
またパラメータθの更新を方策勾配法で解くために、方策勾配定理[1]と呼ばれる定理が存在します。そして方策勾配定理を近似的に実装するアルゴリズムにREINFORCEアルゴリズムと呼ばれるものが存在します。
softmax関数を使用した確率への変換とREINFORCEアルゴリズムに従うと、今回使用したθの更新式が導出されます。またsoftmax関数には、この更新式の導出を解析的に求めやすいという利点もあります。より詳細に数理的背景を知りたい方は[2, 3]をご参照ください。
まとめ
今回は強化学習のアルゴリズムの1つである方策勾配法により、迷路課題を解く部分を実装しました。これで1つ強化学習が実装できたことになります。次回は価値反復法を実装するために必要な知識について解説します。
引用
- [1] Sutton, Richard S., et al. "Policy gradient methods for reinforcement learning with function approximation." Advances in neural information processing systems. 2000.
- [2] これからの強化学習(著)牧野 貴樹ら 森北出版
- [3] 最強囲碁AI アルファ碁 解体新書 深層学習、モンテカルロ木探索、強化学習から見たその仕組み(著)大槻 知史 翔泳社