2018.01.16
作りながら学ぶ強化学習 -初歩からPyTorchによる深層強化学習まで
第4回 迷路を進むエージェントの作成
SEやプログラマ、エンジニア、一般の方を対象に、少しずつ実際にプログラムを作りながら、強化学習および深層強化学習について解説していきます。
本連載をまとめ、さらに多くの記事を追加した書籍『つくりながら学ぶ!深層強化学習』を2018年7月に発売しました!
はじめに
前回は、インストール作業不要ですぐにPythonを実装できるtry Jupyter!の使い方を説明し、今後強化学習の説明で使用する迷路課題の初期状態描画部分を実装しました。
今回は迷路内をランダムに探索してゴールを目指すエージェント(Agent)の実装と、エージェントが迷路内をゴールまで移動した軌跡を動画にするプログラムを実装します。
エージェントの実装
迷路の初期状態描画
前回の記事を参考に、try Jupyter!で新規のPython3ファイルを作成し、ライブラリのimport部分を記入します。前回記事とは1点異なっており、numpyというライブラリもimportしています。
# Jupyterでmatplotlibを使用する宣言と、使用するライブラリの定義 import numpy as np import matplotlib.pyplot as plt %matplotlib inline
次に迷路の初期状態を描画します。2つ目のセルに以下の内容を入力してください。少し長いので、コピー&ペーストしてくださっても構いません。
# 初期位置での迷路の様子
# 図を描く大きさと、図の変数名を宣言
fig = plt.figure(figsize=(5, 5))
ax = plt.gca()
# 赤い壁を描く
plt.plot([1, 1], [0, 1], color='red', linewidth=2)
plt.plot([1, 2], [2, 2], color='red', linewidth=2)
plt.plot([2, 2], [2, 1], color='red', linewidth=2)
plt.plot([2, 3], [1, 1], color='red', linewidth=2)
# 状態を示す文字S0~S8を描く
plt.text(0.5, 2.5, 'S0', size=14, ha='center')
plt.text(1.5, 2.5, 'S1', size=14, ha='center')
plt.text(2.5, 2.5, 'S2', size=14, ha='center')
plt.text(0.5, 1.5, 'S3', size=14, ha='center')
plt.text(1.5, 1.5, 'S4', size=14, ha='center')
plt.text(2.5, 1.5, 'S5', size=14, ha='center')
plt.text(0.5, 0.5, 'S6', size=14, ha='center')
plt.text(1.5, 0.5, 'S7', size=14, ha='center')
plt.text(2.5, 0.5, 'S8', size=14, ha='center')
plt.text(0.5, 2.3, 'START', ha='center')
plt.text(2.5, 0.3, 'GOAL', ha='center')
# 描画範囲の設定と目盛りを消す設定
ax.set_xlim(0, 3)
ax.set_ylim(0, 3)
plt.tick_params(axis='both', which='both', bottom='off', top='off',
labelbottom='off', right='off', left='off', labelleft='off')
# 現在値S0に緑丸を描画する
line, = ax.plot([0.5], [2.5], marker="o", color='g', markersize=60)
エージェントの行動ルールである方策πθ (s,a)の導入
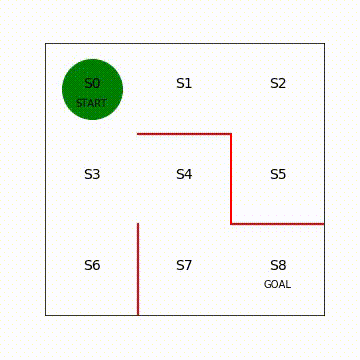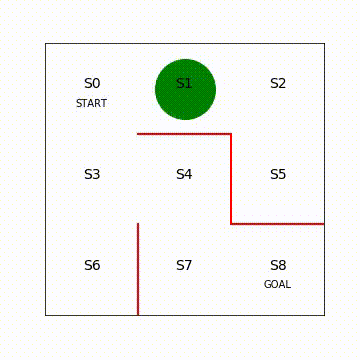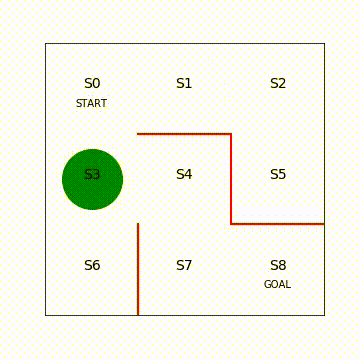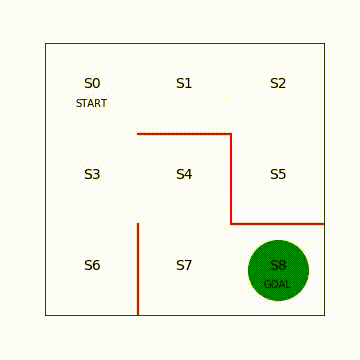
本節では、緑丸で示されたエージェント(図4.3参考)がどのように迷路内を行動するのかを定めたルールである方策(Policy)を設計します。
方策はPolicyのPをギリシャ文字にして、πθ (s,a)と表されます。πθ (s,a)を分かりやすく説明すると、「状態sのときに行動aを採用する確率は、パラメータθで変化する方策πに従います」という意味です。
ここで状態sとはエージェントが迷路内のどの位置にいるのかを示します。今回の迷路の場合はS0からS8までの9つの状態があります。迷路課題以外の場合、例えばロボットであれば現在の姿勢を再現するための関節の角度や速度となり、囲碁や将棋であれば盤面のコマの位置や種類となります。
行動aはその状態でエージェントが実行できる行動を示します。今回の迷路の場合は上、右、下、左へ移動するという4種類の行動があります。ただし赤い壁がある方向へは移動はできません。迷路課題以外の場合、例えばロボットであれば各関節のモータをそれぞれどの程度回転させるかであり、囲碁や将棋であれば次の手でどの位置にどのコマを置くのかになります。
方策πは様々な形で表現されます。例えば関数を使用することもあれば、深層強化学習のようにディープ・ニューラルネットワークで表されることもあります。今回の迷路課題ではもっとも簡単な表現である表形式(Tabler representation)を使用します。表形式は行が状態sを、列が行動aを示し、表の値はその行動を採用する確率を示します。
パラメータθは、方策πが関数の場合は関数内のパラメータであり、ディープ・ニューラルネットワークの場合は素子間の重み(連載後半で詳細を説明します)等です。今回の表形式の場合には、状態sのときに行動aを採用する確率へと変換される値を示します。「確率へと変換される値」という表現はいまいちピンと来ないと思いますが、これから具体例で示します。
方策πθ (s,a)の実装
それでは今回の迷路課題のパラメータθの初期値θ0を決定します。以下の内容を3つ目のセルに記入して実行してください。
# 初期の方策を決定するパラメータtheta_0を設定
# 行は状態0~7、列は移動方向で↑、→、↓、←を表す
theta_0 = np.array([[np.nan, 1, 1, np.nan], # s0
[np.nan, 1, np.nan, 1], # s1
[np.nan, np.nan, 1, 1], # s2
[1, 1, 1, np.nan], # s3
[np.nan, np.nan, 1, 1], # s4
[1, np.nan, np.nan, np.nan], # s5
[1, np.nan, np.nan, np.nan], # s6
[1, 1, np.nan, np.nan], # s7、※s8はゴールなので、方策はなし
])
進める方向には1を、壁があって進めない方向にはnp.nanを代入しています。np.nanは何も入っていない欠損値を示します。
続いて、このパラメータθ0を変換して方策πθ (s,a)を求めます。今回は単純な変換方法を採用し、進める方向に対してθ0の値を割合に変換して確率とします。この変換関数をsimple_convert_into_pi_from_thetaという名前で定義しましょう。
# 方策パラメータthetaを行動方策piに変換する関数の定義
def simple_convert_into_pi_from_theta(theta):
'''単純に割合を計算する'''
[m, n] = theta.shape # thetaの行列サイズを取得
pi = np.zeros((m, n))
for i in range(0, m):
pi[i, :] = theta[i, :] / np.nansum(theta[i, :]) # 割合の計算
pi = np.nan_to_num(pi) # nanを0に変換
return pi
続いて定義した変換関数を実行してθ0から方策πθ (s,a)を求めます。
# 初期の方策pi_0を求める pi_0 = simple_convert_into_pi_from_theta(theta_0)
次のセルでpi_0とだけ入力し、Alt+Enterキーでセルを実行すると以下の図4.1のような結果が表示されます。θ0が割合へと変換されていることが確認できます。
pi_0
以上でエージェントの方策を実装することができました。
エージェントが方策に従いゴールを目指す部分の実装
続いて、方策πθ (s,a)に従って、エージェントを行動させます。1step移動後のエージェントの状態sを求める関数をget_next_sという名前で定義します。
# 1step移動後の状態sを求める関数を定義
def get_next_s(pi, s):
direction = ["up", "right", "down", "left"]
# pi[s,:]の確率に従って、directionが選択される
next_direction = np.random.choice(direction, p=pi[s, :])
if next_direction == "up":
s_next = s - 3 # 上に移動するときは状態の数字が3小さくなる
elif next_direction == "right":
s_next = s + 1 # 右に移動するときは状態の数字が1大きくなる
elif next_direction == "down":
s_next = s + 3 # 下に移動するときは状態の数字が3大きくなる
elif next_direction == "left":
s_next = s - 1 # 左に移動するときは状態の数字が1小さくなる
return s_next
最後に、ゴールにたどり着くまでπθ (s,a)に従ってget_next_sでエージェントを移動させ続けます。まずゴールにたどり着くまで移動し続ける関数goal_mazeを定義します。goal_maze関数はゴールにたどり着くまでに移動した状態の軌跡state_historyを出力するように定義します。
# 迷路を解く関数の定義
def goal_maze(pi):
s = 0 # スタート地点
state_history = [0] # エージェントの移動を記録するリスト
while (1): # ゴールするまでループ
next_s = get_next_s(pi, s)
state_history.append(next_s) # 記録リストに次の状態(エージェントの位置)を追加
if next_s == 8: # ゴール地点なら終了
break
else:
s = next_s
return state_history
それでは定義したgoal_maze関数を実行して方策πθ (s,a)に従いエージェントを移動させ、移動の軌跡をstate_historyに格納します。
state_history = goal_maze(pi_0)
これでゴールするまでのエージェントの移動がstate_historyに格納されました。ゴールするまでにどのような軌跡で、合計何ステップ移動したのか確認しましょう。以下の内容を入力してください。
print(state_history)
print("迷路を解くのにかかったステップ数は"+str(len(state_history)-1)+"です")
するとゴールまでの状態の変化と、要したステップ数が以下の図4.2のように出力されます。エージェントが確率的にランダムに移動しているので、状態の軌跡は実行するたびに変化します。
エージェントの移動を動画で可視化
状態遷移の軌跡に従い迷路内をエージェントが移動する様子を動画にします。次の内容をセルにコピー&ペーストして実行してください。するとエージェントが迷路内を移動する図4.3のような動画が表示されます。
# エージェントの移動の様子を可視化します
# 参考URL http://louistiao.me/posts/notebooks/embedding-matplotlib-animations-in-jupyter-notebooks/
from matplotlib import animation
from IPython.display import HTML
def init():
# 背景画像の初期化
line.set_data([], [])
return (line,)
def animate(i):
# フレームごとの描画内容
state = state_history[i] # 現在の場所を描く
x = (state % 3) + 0.5 # 状態のx座標は、3で割った余り+0.5
y = 2.5 - int(state / 3) # y座標は3で割った商を2.5から引く
line.set_data(x, y)
return (line,)
# 初期化関数とフレームごとの描画関数を用いて動画を作成
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=len(
state_history), interval=200, repeat=False)
HTML(anim.to_html5_video())
入力していただいたコードは2つ内容から構成されています。迷路をエージェントが移動するときに緑丸の中心座標をフレームごとにどう設定するのかを定義し、Pythonの動画描画関数を実行しています。動画の描画方法はPythonの細かいテクニックなので説明は省略します。詳細は、Embedding Matplotlib Animations in Jupyter Notebooks[1]などを参照してください。
動画を見ると、一直線にゴールに向かっておらず、エージェントが迷路内をさまよっていることが分かります。各状態で進める方向にランダムに移動しているためです。今後、エージェントが一直線にゴールに向かうように強化学習で方策を学習させていきます。
最後に今回ここまで実装した内容をダウンロードして保存しておいてください。ダウンロード保存の方法は前回の記事に記載しております。
本日はエージェントの行動ルールである方策πθ (s,a)という概念の導入、迷路課題を対象に表形式で方策πθ (s,a)を実装、エージェントが方策に従いゴールを目指す部分の実装、エージェントの移動軌跡を動画で可視化する内容の実装をしました。次回はエージェントが一直線にゴールに向かうように強化学習で方策を学習させる部分を実装します。
引用
- [1] Embedding Matplotlib Animations in Jupyter Notebooks http://louistiao.me/posts/notebooks/embedding-matplotlib-animations-in-jupyter-notebooks