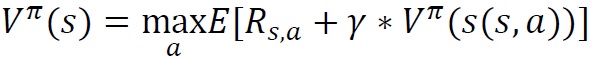本連載をまとめ、さらに多くの記事を追加した書籍『つくりながら学ぶ！深層強化学習』を2018年7月に発売しました！

（上の書籍画像をクリックすると購入サイトに移動できます）

はじめに

　前回は、強化学習のアルゴリズムの一種である方策勾配法を用いて、迷路内をエージェントが一直線にゴールへ向かうように方策を学習させました。

　今回は価値反復法のアルゴリズムを実装するために必要な知識、概念、専門用語を解説します。報酬、行動価値、状態価値、ベルマン方程式、マルコフ決定過程について説明します。

報酬の導入

　強化学習のアルゴリズムの１つである価値反復法を実装するために必要な知識を解説します。

　アルゴリズムの名前に価値という言葉がつくため、まずはじめに価値を定義する必要があります。価値とは、例えばダイヤモンドの場合「換金したときに何円になるのか」で表されます（基本的には）。つまり価値を決めるにはお金のような概念が必要になります。

　価値反復法にお金は出てきませんが、お金の代わりに報酬という概念を使用します。例えば迷路課題であればゴールをしたときに報酬を与えます。またロボットの歩行であれば転ばずに歩けている間、毎ステップ報酬を与えます。囲碁であれば勝負に勝てば報酬を与えます。この、とある時刻tでもらえる報酬を即時報酬（immediate reward）R_tと呼びます。なお強化学習で報酬R_tをどのような値にするのかは、課題に合わせて自分で設定することになります。

　また、今後未来に渡って得られるであろう報酬の合計を報酬和G_tと呼びます。

G_t = R_t+1 + R_t+2 + R_t+3 + …

 

　ただし、時間の経過を考える必要があるので、利率を考慮する必要があります。例えば、現在の1万円は銀行に10年間預けておけば、毎年の金利分だけ複利効果でお金が増えて、10年後には1万円とちょっとに増えています。これは逆に考えれば、10年後の1万円は現在の価格で考えると1万円よりもちょっと小さくなります。このように未来の報酬は割り引いて考えることを時間割引と呼び、その割引率を𝛾 で表します。なお、𝛾 は0から1の間の数になります。

　少し脱線となりますが、2017年のノーベル経済学賞を受賞したセイラー教授（Richard H. Thaler）の研究は「行動経済学」と呼ばれ、その一例として人間は将来得られる価値を必要以上に割り引いて考える傾向にあることを紹介しています（例えば1年後の12,000円よりも今日もらえる10,000円のほうが魅力的に感じられる）[1]。また脳科学の研究では、そのように人間が行動してしまうのは、脳内の線条体という部位と、主にセロトニンという物質が影響していると報告されています[2,3]。

　利率や複利効果を考えて将来にわたる報酬合計を考える際には、時間割引率を考慮した割引報酬和（dicounted total reward）G_tを使用します。

G_t = R_t+1 + 𝛾 R_t+2 + 𝛾 ² R_t+3 + …

価値の導入

　報酬を定義できたので、続いて価値という概念を強化学習に導入します。価値反復法では行動価値（action Value）と状態価値（state Value）という2種類の価値を定義します。図6.1の迷路課題を例にこれらを解説します。ゴールである状態S8にエージェント（緑丸）が辿り着いた瞬間、報酬R_t = 1がもらえると設定します。

図6.1 迷路課題の図

　はじめに行動価値について説明します。現在エージェントが迷路のS7にいると仮定してください。S7から右に移動すればゴールにたどり着くことができます。つまり状態 s = S7で、行動 a = 右 だった場合、S7→S8と移動し次のステップでゴールにたどり着き、報酬R_t+1=1を手にすることができます。

　これを式で表します。方策πの元で、行動価値は行動価値関数Q^π(s, a)と書かれます。行動は（上、右、下、左より）、右へ移動するのはa = 1だったので、

Q^π(s=7, a=1) = 1

となります。なお価値反復法における方策πの詳細については次回説明します。

　では今エージェントが状態 s = S7 にいて、行動 a = 上 だった場合、行動価値関数Q^π(s, a)はどうなるのでしょうか？エージェントはS4へと移動してゴールから遠ざかります。すると、S4からゴールするにはS7→S4→S7→S8（ゴール）とゴールまで2ステップ余分に時間がかかります。これを式で表すと、

Q^π(s = 7, a = 0) = 𝛾 ² *1

となります。つまりゴールにたどり着くために2ステップ多めにかかるのでその時間分だけ割り引いた報酬が得られると考える必要があります。

　続いて状態価値について説明します。状態価値とは状態sにおいて方策πに従って行動することで、その後将来にわたって得られることが期待される割引報酬和G_tです。状態sの状態価値関数をV^π(s)と書きます。

　例えば、エージェントがS7にいる場合に右に移動すればゴールして報酬1を手に入れることができるので、

V^π(s = 7) = 1 

となります。また、エージェントがS4にいる場合は下に移動して、S7にたどりつき、右に移動してゴールできるので、状態価値関数の値は

V^π(s = 4) = 𝛾 *1

となります。

エージェントがS4にいるときの状態価値関数は、次のような表現をすることもできます。

V^π(s = 4) = R_t+1 + 𝛾 * V^π(s = 7)

ここで、R_t+1は状態S4で得られる報酬ですが、ゴールのS8以外では報酬は得られないので、上式ではR_t+1 = 0です。

つまり、

V^π(s = 4) = 0 +𝛾 * V^π(s = 7) = 𝛾 * 1

となり、最初の式と同じ状態価値の値になります。

ベルマン方程式とマルコフ過程

　先ほど説明した価値関数の式をより一般的な書き方で表すと

と書くことができ、これをベルマン方程式と呼びます。

なんだか突然難しそうな式が出てきましたが簡単な言葉で説明します。左辺にある状態sでの状態価値Vは、右辺が最も大きくなる行動aをとったときに期待される値です。右辺のR_s,aは状態sで行動aをとったときに、得られる即時報酬です。迷路の場合はゴールにたどり着く場合以外は全部0です。左辺のV^πの中にあるs(s,a)は状態sで行動aを採用して移動した先の新たな状態sを示しています。この新たな状態sでの状態価値Vに時間割引率を掛けた項と、即時報酬R_s,aの和が現在の状態価値になります。

　このベルマン方程式が成り立つための前提条件として、学習したい対象がマルコフ決定過程（Markov Decision Process）である必要があります。これまた難しそうな言葉ですが、なんら難しいことはありません。マルコフ決定過程とは、次のステップの状態s_t+1が現在の状態sと選択した行動aで確定するシステムのことです。つまり先ほどのベルマン方程式で説明した「右辺のs(s,a)が状態sで行動aをとったときに移動する新たな状態sを示す」という部分がきちんと成り立つということを示しています。

　ではマルコフ決定過程ではないものは何かというと、現在の状態s以外に過去の状態にも影響されて次の状態s_t+1が決まるようなシステムです。

価値反復法における方策と価値の決定方法

　ここまで報酬と行動価値、状態価値を説明してきましたが、それではいったいどうやって行動価値や状態価値、そして行動を決める方策を学習すれば良いのかという疑問が残ります。

　価値反復法において行動価値、状態価値を決めるアルゴリズムの代表例には、Sarsa、Q学習、モンテカルロ法があります。また方策は行動価値に基いて決める方法が一般的です。これらのアルゴリズムについて次回以降に解説していきます。

まとめ

　今回は価値反復法のアルゴリズムを実装するために必要な、報酬、行動価値、状態価値、ベルマン方程式、マルコフ決定過程について説明しました。

　次週は、TD誤差、探索と利用のトレードオフについて解説したのちに、Sarsaアルゴリズムで迷路課題を解く部分を実装します。

引用

• [1] 実践 行動経済学（著）リチャード・セイラーら 日経BP社
• [2] Tanaka, Saori C., et al. "Neural mechanisms of gain?loss asymmetry in temporal discounting." Journal of Neuroscience 34.16 (2014): 5595-5602.
• [3] 脳の中の経済学（著）大竹 文雄ら ディスカヴァー・トゥエンティワン