プログラミング初心者のMさんが、ビジュアルプログラミング教材「プログラミングゼミ」を学びながら、プログラミング的思考と技術を習得していくストーリーです。
最初は嫌々ながらプログラミング教室に通いはじめたMさん。
なんだかんだ言いながらも楽しくパズルゲームで遊んで、いや、勉強しているようですよ。

 

 

	だんだん慣れてきた。このパズルは簡単！
	いいですねー！ 楽しくなってきたでしょう？ でも、簡単すぎてもつまらないので、応用課題を出してみましょうか？
	はいっ！ 今日は調子がいいので、ぜひやってみたいです。
	では、「もんだい5-2」をもう一度開いてください。
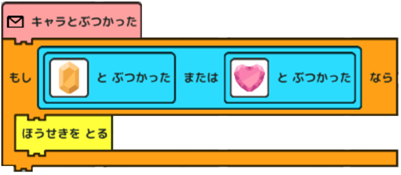
	はい。「オレンジ」と「ピンク」の宝石を取るプログラムですね。 こんなふうにプログラムしたんですけど。

 

 

	素晴らしい。満点の答えです！ では、これと同じ動作をするプログラムを「または」ブロックを使わずに作ってみてください。
	「または」ブロックを使わずに？ はい。やってみます。

   

	できました！
	おおっ、調子がいいですね。 どんなプログラムか見せてもらってもいいですか？
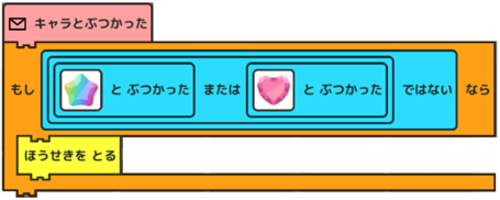
	はい。このようにしました。

 

 

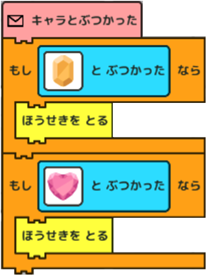
	そうそう、これでいいんです。確かに同じ動作をしますよね。
	いろんな方法があるんですね。
	その通りです。別の方法を見つけるのも楽しいですよ。

「～ではない」が重なると難しくなる！？

 

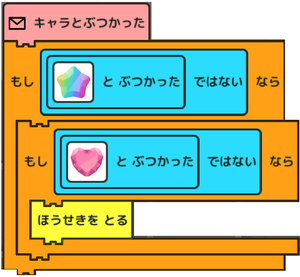
	じゃあ、次の応用課題に取り組んでみてください。 「もんだい5-4」の画面にして、そらもんが、「にじいろ」と「ピンク」以外の宝石をとるプログラムを作って下さい。
	「にじいろ」と「ピンク」は取らないで、それ以外の宝石を取るということですね。 やってみます。

   

「にじいろ」とぶつかってないときか、「ピンク」とぶつかってないときに宝石を取るんだから、…こうかな？

 

 

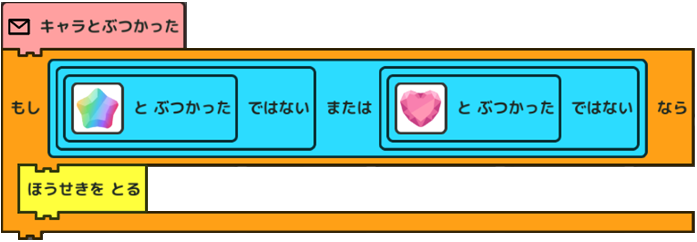
	先生、できました！
	早いですね。 では、プログラムを動かしてみてください。
	はい。

 

 

 

 

	あれっ？ 全部の宝石を取っちゃった(´;ω;｀) どうしてうまくいかないんだろう？
	どうしてだと思いますか？ では、どんなブロックを取りますか？
	「にじいろ」以外全部です。
	正解です。 では、 では、どんなブロックを取りますか？
	「ピンク」以外全部です。
	では、それを「または」でつなぐとどうなりますか？
	で「にじいろ」以外全部取って、 で「ピンク」以外全部取るので、…あっ、確かに、全部の宝石を取ってしまいますね。 じゃあ、どうすればいいんですか？
	もうほとんど答えにたどり着いてますよ！ で「にじいろ」以外全部取って、 で「ピンク」以外全部取りますよね。 他の色の宝石は、その「どちらにも」入ってますよね。 「どちらにも」がポイントですよ。 よーく考えてみてください。
	「どちらにも」なので、「または」ではなく「かつ」ですね！ 分かりました。 では、「かつ」を使ってやってみようっと。 あれ、先生、「かつ」ブロックがありません！
	そこまで気付いたのなら、十分ですよ。 このパズルには「かつ」ブロックはありませんが、レベルが上がっていくと、「かつ」ブロックも出てきますので、その時使えるようになっていればいいんです。
	じゃあ、この応用課題は無理だということですか？
	いえ、「かつ」ブロックを使わなくてもできますよ。 ヒントを1つ。 さっき、「もんだい5-2」でもやった別パターンを思い出してください。
	えーっと。さっきは「または」の代わりに「もしも」ブロックを2つ続けたのか。 では、同じようにやってみようかな。

   

 

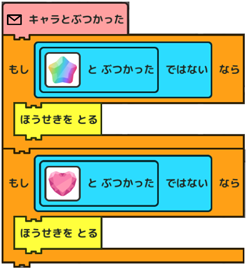
	これでやってみると、どうなるかな？ あれっ？うまくいかない。さっきと同じで全部取っちゃった。
	苦戦してますね。 でも、これも収穫ですよ。
	どういうことですか？
	次の公式が成り立つということです

 

 

	なるほど！ 同じ処理を別パターンでやる場合の公式ということですね。 確かにこのことを覚えておくと、無駄な回り道をしなくて済みますね！
	「かつ」というのは、「両方の条件を満たす」という意味ですよね。 両方の条件を同時に満たすには、どうすればいいと思いますか？
	「両方の条件を同時に満たす」？ という条件を満たして，さらに という条件を満たすのか。 ということは…， あっ！「もし」の中にもう一つ「もし」を入れてみたらいいのかな？

 

 

 

 

 

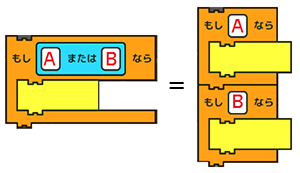
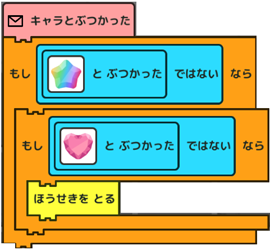
	やったー！できた。
	その通りです！ 結構頭を使いましたね。 ここからも、公式を導くことができます。

 

 

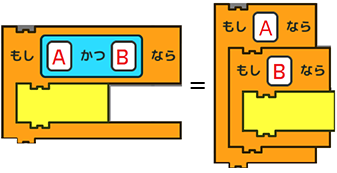
	なるほど！ ひとつずつ覚えていこうっと。
	いい心がけです。頑張ってくださいね。 でも、もっと簡潔にできるパターンもあるんですよ！
	えっ、どんなのですか？

 複雑な論理演算をスマートに！- 「ド・モルガンの法則」

これです！

 

 

 

 

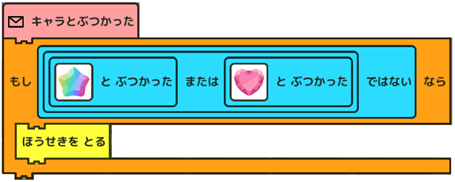
	たしかに！ ちゃんと動きますね。 これは、どういう書き換えですか？
	ということです。 数学的には、「ド・モルガンの法則」といいます。
	ド、…ドモル…、何ですか？
	「ド・モルガンの法則」です。 高校数学で学ぶ内容ですね！
	えーっ、数学は苦手でした。 全然覚えてないんですけど。
	大丈夫、そんなに難しいことではありません。 次の図で、「AまたはB」は、何色の部分ですか？

 

 

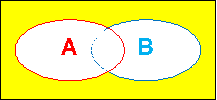
	白の部分ですね。
	その通りです。 では、「（AまたはB）でない」はどこですか？
	黄色の部分ですね。
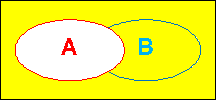
	では、「Aでない」は？

 

ここですね！黄色の部分。

 

 

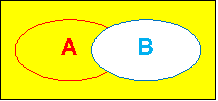
	その通り！ では、「Bではない」は？
	ここです！

 

 

では、これらの３つの図を並べてみましょうか。

 

 

	何か気付きませんか？
	あっ、確かに。 最初の2つの図でどちらも黄色の部分が、最後の図になっていますね！

その通りです。 これで、イメージが掴めましたね。 では、もう一度、今回作った、同じ動きをするプログラムを並べてみましょうか。

 

 

	どちらが簡単ですか？
	それは後の方です。 その方が分かりやすいし、見やすいです。

	ですよね。 そして、プログラムが短いので、前回学んだ「最適化」されているといえます。
	なるほど、便利なんですねー。
	ド・モルガンの法則を活用できると、プログラムを最適化しやすくなるんですよ。 特に、色々な条件が絡んでいるときに威力を発揮するんです。 私も、数学で学んだときには、難しいと感じて、スルーしてたんですが、 プログラミングをするのにとても役立つので、今では重宝していますよ。
	そうなんですね。 数学は苦手だったので不安でしたが、よく分かりました！

 

今回のパズル、いかがでしたか？
こども用の「プログラミングゼミ」ですが、結構奥が深いですね。
プログラミングをしていると今回のように「または」とか「かつ」という考え方がたくさん出てきます。
頭の中で考えるだけだと混乱してしまうことがあるので、分からなくなったときは 今回のように図を描きながら考えを整理してみると良いですね！
さて次回は、「繰り返し（ループ）」処理に挑戦してみましょう。