2017.03.17
AtCoderでの基本の考え方を学ぼう![第5回]
前回は、競技プログラミングにおけるもっとも基礎である、標準入出力について学びました。
今回からは、実際に問題を解けるようになるためにどのような考え方をすれば良いのか、身に着けるための内容を説明していきたいと思います。
基本は全探索!
AtCoderはアルゴリズムのコンテストなので、何か工夫をして問題を解きたくなってしまうことが多いかもしれません。
ですが、アルゴリズムの最も基本的な部分は 全探索です。
基本的に、現代のコンピュータは計算速度が無茶苦茶速いですので、その計算速度を活用しない手はありません。
人間が真面目に考えると極めて時間がかかってしまうような問題でも、コンピュータを使えば高速に計算することが可能であることが多いです。
難しいアルゴリズムを考えるにしても、まず全てのパターンをしらみつぶしに探索する全探索ができないとお話になりません。
| アルゴリズム名 | 説明 |
|---|---|
| 線形探索 | 上で紹介したもの。単純にループを回し、データの頭から探索していく |
| 2次元探索 | 線形探索上で線形探索をするもの。3次元や4次元ももちろんあり得る |
| 深さ優先探索 | 単純なループなどでは探索することが難しいのに対し、 |
| 幅優先探索 | 上で紹介した深さ優先探索と似ているが、探索順序の違うもの。こちらは一般にキューを用いる |
| bit全探索 | 使う、使わないを整数の1つのbitにまとめることで、1つの整数のループで、複数のフラグのon/offを全探索する |
それぞれのアルゴリズムの詳しい説明については今回は避けますが、競技プログラミングを最初に始める上で最初これらの知識がなくても全く問題はありません。
コンテストに出場していくうちに、こういったアルゴリズムが徐々に身に着いていくものなのです。
全探索の問題
先の表で一番大切なのは線形探索です。全てのデータを順番にforループなどで調べるだけなのですが、少し高度な全探索についての問題を今回出題しようと思います。
問題に専門用語っぽいものがいくつか出てきますが、わからない場合は読み飛ばしてしまっても大丈夫だと思います。
問題
制約
入力
解説
専門用語がたくさん出てきてしまったので、訳が分からないという人も多いかと思います。
グラフというのは、丸と棒で繋がったような図の事だと思ってください。丸が頂点で、棒が辺です。
棒が矢印の場合は一方通行となり、そのような辺を含むグラフを有向グラフと言います。今回は矢印ではなく両方向に行き来できるので、 無向グラフです。
無向グラフとして、例えば以下のようなものがあったとします。

その中の「パス」というのは経路のことなのですが、その1つは以下のような経路になります。

他にも、次のようなパスが存在します。

このようなパスのうち、「頂点1から始まるものがいくつあるか」を求める問題ということです。
回答
この問題は全てのパスを求める問題です。アルゴリズムの基本は全探索。あり得るパスを全探索してその個数を求めてしまえば良いわけですね。
……と言ってしまうと簡単ですが、どう列挙すれば良いのか、というのがこの問題の難しいところだと思います。
まず「2つのパスが違うとはどういうことか」というのを明確にしましょう。
 |
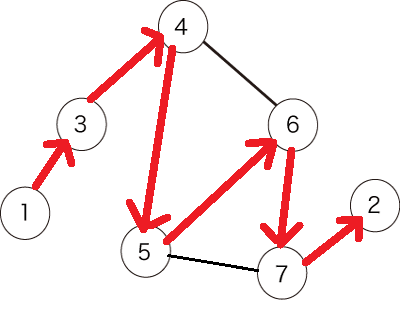 |
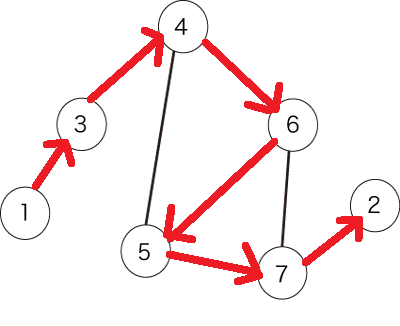
上記の2つのパスは何が違うのでしょうか?
答えは簡単「訪れる頂点の順序」が違います。
・ 1つ目のパスは、{1,3,4,6,5,7,2}という順番で移動しています。
・ 2つ目のパスは、{1,3,4,5,6,7,2}という順番で移動しています。
この頂点の順序が違うからこそ、違うパスだと言えるわけですね。
ここまで書けば、どのような数列を全探索すれば良いかわかったかもしれません。求める数列は、以下の3つの条件を満たしている必要があります。
・ 1 から始まる 7つの要素の数列である。
・ 1 から 7 が 1回ずつ出現する。
・ 隣り合う2つの数が表す頂点どうしの間に辺が存在する。
この条件を用いて探索を行えば良いわけです。
実は上の2つの条件だけであれば、C++ならば next_permutation という関数を使うと簡単に列挙することができます。
ですが今回は、汎用性の高い再帰関数を用いた探索例を示しておきます。
なお、再帰関数を使った全探索を、深さ優先探索と呼びます。非常に使用頻度の高いアルゴリズムなのでぜひ覚えてください。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 | #include #include using namespace std;// 既にその頂点を使っているかどうか管理する配列vector used;// 接続状況を格納する配列vector connect;int N, M;// パスを全探索する関数// now: 今見ている頂点// depth: 今まで列挙した頂点数int dfs(int now, int depth) { // 使用済みであれば return if (used[now]) return 0; // depthがNなら有効なパスなので、1 を返す if (depth == N) return 1; // 使用済みフラグを立てる used[now] = 1; int ans = 0; // 全部の遷移先をチェックする for (int i = 0; i < N; i++) { //nowから繋がっている頂点であれば、遷移を試す if (connect[now][i]) ans += dfs(i, depth + 1); } // 使用済みフラグを折る used[now] = 0; return ans;}int main() { // 入力を受け取る cin >> N >> M; vector a(M), b(M); for (int i = 0; i < M; i++) { cin >> a[i] >> b[i]; // 1から始まると使いづらいので、1引いた値を格納する a[i]--; b[i]--; } // 配列の初期化 used = vector(N, 0); connect = vector(N, vector(N, 0)); for (int i = 0; i < M; i++) { // 配列に反映させる connect[a[i]][b[i]] = connect[b[i]][a[i]] = 1; } // 0番から始まるパスの種類を列挙し、出力する cout << dfs(0, 1) << endl;} |
おわりに
全探索と言ってもいろいろな種類があること分かっていただけたでしょうか?
「単純に全ての要素を列挙する」というだけでも難しい処理はたくさんあります。
今回の問題のような「順列列挙」だけでなく、組み合わせの列挙など全探索が難しいケースは色々と存在します。
様々な全探索の手法を覚えることによって、これらの問題に対しても適切な全探索のコードが書けるようになるかと思います。
次回は今回説明した全探索を前提として全探索が間に合わない場合にどうしたら良いか、という計算量改善の工夫の仕方について解説していきたいと思います。
次回の記事もお楽しみに!




