2018.02.14
作りながら学ぶ強化学習 -初歩からPyTorchによる深層強化学習まで
第8回 Q学習の実装
SEやプログラマ、エンジニア、一般の方を対象に、少しずつ実際にプログラムを作りながら、強化学習および深層強化学習について解説していきます。
本連載をまとめ、さらに多くの記事を追加した書籍『つくりながら学ぶ!深層強化学習』を2018年7月に発売しました!
はじめに
前回は価値反復法のアルゴリズムの1つSarsaで迷路課題を解くコードを実装しました。今回は価値反復法の別のアルゴリズムであるQ学習について解説し、同様に迷路を解くコードを実装します。
Q学習とは
Q学習の更新式
Q学習(Q-learning)はSarsaと同じく価値反復法による強化学習のアルゴリズムです。Sarsaと異なる点は1つだけで、行動価値関数の更新式が違います。
Sarsaの場合行動価値関数の更新式は、
で表されました。一方でQ学習の場合行動価値関数の更新式は
で表されます。
Sarsaの場合は更新時に暫定的に次の行動at+1を求め、更新に使用していました。一方Q学習は状態st+1での最も大きい行動価値関数の値を更新に使用します。
SarsaとQ学習の定性的な違い
Sarsaは行動価値関数Qの更新に次の行動at+1を使用するため、行動価値関数の更新がat+1を求める方策(ε-greedy法)のパラメータ ε に依存するという特徴があります。このような特性を方策オン型と呼びます。そのため、ε を計画的に減らすなどしないと行動価値関数がきちんと学習できません。
一方でQ学習は行動価値関数Qの更新にε-greedy法のパラメータεなど行動決定方法(方策)は依存しません。このような特性を方策オフ型と呼びます。ε-greedy法から生まれるランダム性が更新式に入らない分、行動価値関数の収束がSarsaよりも早いという特徴があります。
とはいえQ学習にε-greedy法が関係ないわけではなく、Sarsaと同じく方策の決定にはε-greedy法を使用します。そうしないと、例えば迷路であれば常に現在の行動価値関数が最大の方向へしか移動せず、未知の状態を探索してくれないからです。ですがSarsaのときのようにパラメータ ε を試行数(エピソード数)に従って小さく変化させなくても、Q学習は最適な方策価値関数に落ち着くことが示されています[1]。
結局SarsaとQ学習のどちらの方が良い手法なのかは実は行動価値関数の更新と、方策のε-greedy法のパラメータの組み合わせで決まるため、確定的にこちらがおすすめですとは証明されてはいないようです。
Q学習の実装
Q学習による更新を実装
Q学習の実装は前回のSarsaの更新部分を書き換えるだけとなります。
# Q学習による行動価値関数Qの更新
def Q_learning(s, a, r, s_next, Q, eta, gamma):
if s_next == 8: # ゴールした場合
Q[s, a] = Q[s, a] + eta * (r - Q[s, a])
else:
Q[s, a] = Q[s, a] + eta * (r + gamma * np.nanmax(Q[s_next,: ]) - Q[s, a])
#Q[s, a] = Q[s, a] + eta * (r + gamma * Q[s_next, a_next] - Q[s, a])
return Q
それに合わせて、実行部分も関数Sarsaから関数Q_learningへと書き換えます。
# Q学習で迷路を解く関数の定義、状態と行動の履歴および更新したQを出力
def goal_maze_ret_s_a_Q(Q, epsilon, eta, gamma, pi_0):
s = 0 # スタート地点
s_a_history = [[0, np.nan]] # エージェントの移動を記録するリスト
while (1): # ゴールするまでループ
[a, s_next] = get_action_and_s_next(s, Q, epsilon, pi_0)
s_a_history[-1][1] = a
# 現在の状態(つまり一番最後なのでindex=-1)に行動を代入
s_a_history.append([s_next, np.nan])
# 次の状態を代入。行動はまだ分からないのでnanにしておく
# 報酬を与え, 次の行動を求めます
if s_next == 8:
r = 1 # ゴールにたどり着いたなら報酬を与える
a_next = np.nan
else:
r = 0
# 価値関数を更新
Q = Q_learning(s, a, r, s_next, Q, eta, gamma)
# 終了判定
if s_next == 8: # ゴール地点なら終了
break
else:
s = s_next
return [s_a_history, Q]
前回のコードとまったく同じでは面白くないので、Q学習で迷路を解きながら、各エピソードでの状態価値関数Vの値を求めるように少し変更を加えましょう。
まず初期のQ関数の値が大きいと描画しにくいので0.1をかけてQの値を小さくしておきます。
# 初期の行動価値関数Qを設定 [a, b] = theta_0.shape # 行と列の数をa, bに格納 Q = np.random.rand(a, b) * theta_0 * 0.1 # *theta0をすることで要素ごとに掛け算をし、Qの壁方向の値がnanになる
そしてQ学習で迷路を解く部分では、各エピソードでの状態価値関数の値を変数Vに格納していくようにします。
# Q学習で迷路を解く
eta = 0.1 # 学習率
gamma = 0.9 # 時間割引率
epsilon = 0.5 # ε-greedy法の初期値
v = np.nanmax(Q, axis=1) # 状態ごとに価値の最大値を求める
is_continue = True
episode = 1
V=[] # エピソードごとの状態価値を格納する
V.append(np.nanmax(Q, axis=1)) # 状態ごとに行動価値の最大値を求める
while is_continue: # is_continueがFalseになるまで繰り返す
print("エピソード:" + str(episode))
# ε-greedyの値を少しずつ小さくする
epsilon = epsilon / 2
# Q学習で迷路を解き、移動した履歴と更新したQを求める
[s_a_history, Q] = goal_maze_ret_s_a_Q(Q, epsilon, eta, gamma, pi_0)
# 状態価値の変化
new_v = np.nanmax(Q, axis=1) # 状態ごとに行動価値の最大値を求める
print(np.sum(np.abs(new_v - v))) # 状態価値関数の変化を出力
v = new_v
V.append(v) # このエピソード終了時の状態価値関数を追加
print("迷路を解くのにかかったステップ数は" + str(len(s_a_history) - 1) + "です")
# 100エピソード繰り返す
episode = episode + 1
if episode > 100:
break
実行すると図8.1のようにエピソード、状態価値Vの変化の絶対値和、かかったステップ数が出力されます。
図8.1 迷路内の探索とQ学習による更新の実行結果
Q学習による状態価値関数の変化を可視化
最後に試行(エピソード)ごとに状態価値関数がどのように変化していくのかを可視化しましょう。前回までの迷路をエージェントが移動するコードを少し書き換えます。
# 状態価値の変化を可視化します
# 参考URL http://louistiao.me/posts/notebooks/embedding-matplotlib-animations-in-jupyter-notebooks/
from matplotlib import animation
from IPython.display import HTML
import matplotlib.cm as cm # color map
def init():
# 背景画像の初期化
line.set_data([], [])
return (line,)
def animate(i):
# フレームごとの描画内容
# 各マスに状態価値の大きさに基づく色付きの四角を描画
line, = ax.plot([0.5], [2.5], marker="s",
color=cm.jet(V[i][0]), markersize=85) # S0
line, = ax.plot([1.5], [2.5], marker="s",
color=cm.jet(V[i][1]), markersize=85) # S1
line, = ax.plot([2.5], [2.5], marker="s",
color=cm.jet(V[i][2]), markersize=85) # S2
line, = ax.plot([0.5], [1.5], marker="s",
color=cm.jet(V[i][3]), markersize=85) # S3
line, = ax.plot([1.5], [1.5], marker="s",
color=cm.jet(V[i][4]), markersize=85) # S4
line, = ax.plot([2.5], [1.5], marker="s",
color=cm.jet(V[i][5]), markersize=85) # S5
line, = ax.plot([0.5], [0.5], marker="s",
color=cm.jet(V[i][6]), markersize=85) # S6
line, = ax.plot([1.5], [0.5], marker="s",
color=cm.jet(V[i][7]), markersize=85) # S7
line, = ax.plot([2.5], [0.5], marker="s",
color=cm.jet(1.0), markersize=85) # S8
return (line,)
# 初期化関数とフレームごとの描画関数を用いて動画を作成
anim = animation.FuncAnimation(
fig, animate, init_func=init, frames=len(V), interval=200, repeat=False)
HTML(anim.to_html5_video())
状態価値関数が変化していく様子を図8.2に動画で可視化します。カラーマップのjet形式を採用しており、状態価値が低いと濃い青色です。状態価値が高くなるにつれて濃い赤色へと変化します。最初、ゴールであるS8のみ価値が大きく濃い赤色をしていますが、その他のマスは状態価値の値が小さく青色になっています。エピソードを繰り返しQ学習が進むにつれて、S7、S4、S3、S1とゴールから逆向きにだんだんとゴールへの道筋が青色から赤色に変化していく様子が分かります。完全に濃い赤色にならないのは時間割引率γで状態価値が割り引かれているからです。この図で重要な点が2つあります。1つ目は報酬が得られるゴールから逆向きに状態価値が学習されていくイメージを持つこと、2つ目は学習後にはスタートからゴールへの道筋が生まれるということです。
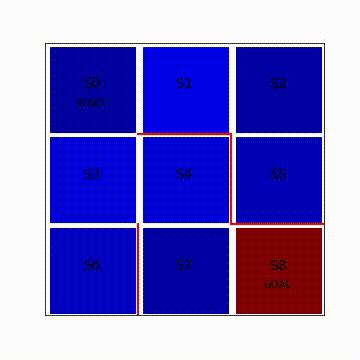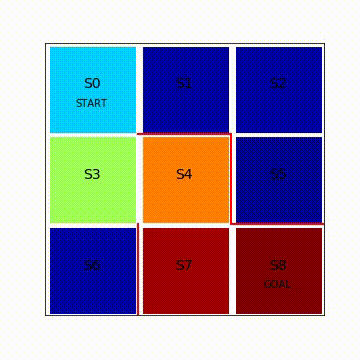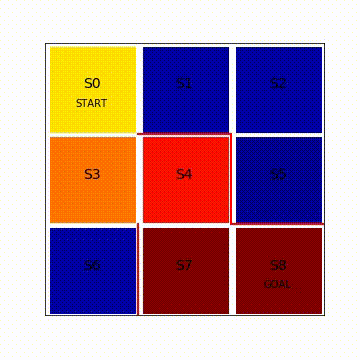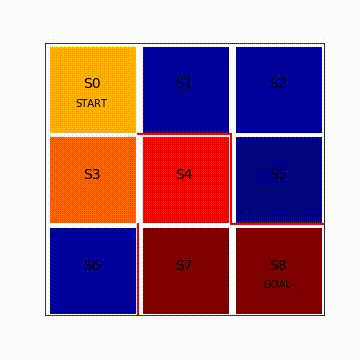
図8.2 Q学習による状態価値関数の変化の様子(再生繰り返し)
以上、価値反復法のQ学習アルゴリズムにより迷路を解く強化学習プログラムの実装と状態価値の可視化を紹介しました。
まとめ
今回は価値反復法のQ学習により、迷路課題を解くアルゴリズムを実装しました。今回までで基礎的な強化学習の知識の紹介と実装は終了となります。ここまでを理解できれば強化学習の知識と実装のベース能力がついたことになります。 次回からより高度な強化学習課題へ取り組みます。次回は、倒立振子と呼ばれる制御課題をOpenAI GymのCartPoleと呼ばれるプログラムを使用して実装するための環境構築について解説します。
引用
[1] Watkins, Christopher JCH, and Peter Dayan. "Q-learning." Machine learning 8.3-4 (1992): 279-292.